Overview of Regression 📖
MATH 4780 / MSSC 5780 Regression Analysis
Department of Mathematical and Statistical Sciences
Marquette University
What is Regression
Regression is a statistical technique for investigating and modeling the relationships between variables.
Relationship as Functions
- Represent relationships between variables using functions \(y = f(x)\).
- Plug in the inputs and receive the output.
- \(y = f(x) = 3x + 7\) is a function with input \(x\) and output \(y\).
- If \(x = 5\), \(y = 3 \times 5 + 7 = 22\).
Different Relationships
Can you come up with any real-world examples describing relationships between variables deterministically?
Different Relationships


Relationship between Variables is Not Perfect
Can you provide some real examples that the variables are related each other, but not perfectly related?
Relationship between Variables is Not Perfect
💵 In general, one with more years of education earns more.
💵 Any two with the same years of education may have different annual income.

Variation around the Function/Model
What are the unexplained variation coming from?
-
Other factors accounting for parts of variability of income.
- Adding more explanatory variables to a model can reduce the variation size around the model.
- Pure measurement error.
- Just that randomness plays a big role. 🤔
What other factors (variables) may affect a person’s income?
your income = f(years of education, major, GPA, college, parent's income, ...)
Regression Model
-
\(Y\): response, outcome, label, dependent variable, e.g.,
income -
\(X\): predictor, covariate, feature, regressor, explanatory/ independent variable, e.g.,
years of education, which is known and fixed.
- Explain the relationship between \(X\) and \(Y\) and make predictions through a model \[Y = f(X) + \epsilon\]
-
\(\epsilon\): irreducible random error
- independent of \(X\)
- mean zero with some variance.
- \(f(\cdot)\): fixed but unknown function describing the relationship between \(X\) and the mean of \(Y\).
In Intro Stats, what is the form of \(f\) and what assumptions you made on the random error \(\epsilon\) ?
- \(f(X) = \beta_0 + \beta_1X\) with unknown parameters \(\beta_0\) and \(\beta_1\).
- \(\epsilon \sim N(0, \sigma^2)\).
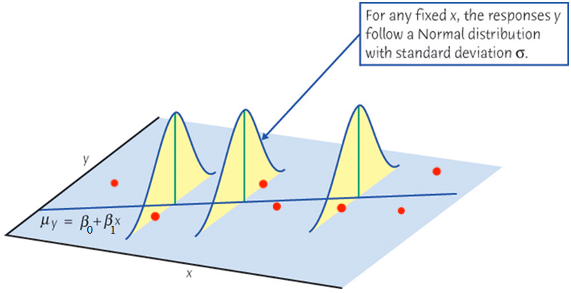
True Unknown Function \(f\) of the Model \(Y = f(X) + \epsilon\)
-
Blue curve: true underlying relationship between (the mean)
incomeandyears of education. - Black lines: error associated with each observation
Big problem: \(f(x)\) is unknown and needs to be estimated.
Why Estimate \(f\)? Prediction for \(Y\)
- Prediction: Inputs \(X\) are available, but the output \(Y\) cannot be easily obtained. We predict \(Y\) using \[ \hat{Y} = \hat{f}(X), \] where \(\hat{f}\) is our estimate of \(f\), and \(\hat{Y}\) represents the resulting prediction for \(Y\).
In Intro Stats, what is our estimated regression function \(\hat{f}\)?
- \(\hat{Y} = \hat{\beta}_0 + \hat{\beta}_1X\).
- \(\hat{f}\) is often treated as a black box.
Why Estimate \(f\)? Inference for \(f\)
- Inference: Understand how \(Y\) is affected by \(X\).
- \(\hat{f}\) cannot be treated as a black box. We want to know the exact form of \(f\).
We are interested in
-
Which covariates are associated with the response?
👉 Doage,education level,gender, etc affectsalary?
-
What is the relationship between the response and each covariate?
👉 How muchsalaryincreases/decreases asageincreases one unit?
-
Can the relationship be adequately summarized using any equation?
👉 The relationship betweensalaryandageis linear, quadratic or more complicated?
How to Estimate \(f\)?
- Observations \(\{(x_1, y_1), (x_2, y_2), \dots, (x_n,y_n)\}\): training data to train or teach our model to learn \(f\).
- Use test data to test or evaluate how well the model makes inference or prediction.
- Models are characterized as either parametric or nonparametric.
-
Parametric methods involve a two-step model-based approach:
- 1️⃣ Make an assumption about the functional form, or shape of \(f\), e.g. linear regression \[ f(X) = \beta_0 + \beta_1X_1 \]
- 2️⃣ Use the training data to fit or train the model, e.g., estimate the parameters \(\beta_0, \beta_1\) using (ordinary) least squares.
-
Nonparametric methods do not make assumptions about the shape of \(f\).
- Seek an estimate of \(f\) that gets close to the data points without being too rough or wiggly.
Parametric vs. Nonparametric Models
Parametric (Linear regression)
Nonparametric (LOESS)
Parametric vs. Nonparametric Models
- Parametric: Assumptions on \(f\) with unknown parameters.
- Nonparametric: No assumptions on \(f\) (may have no closed form).
Linear vs. Nonlinear Models
-
Linear Regression: \(Y\) is linear in unknown parameters, NOT predictors.
- \(Y = \beta_0 + \beta_1X + \epsilon\)
- \(Y = \beta_0 + \beta_1X + \beta_2X^2 + \epsilon\)
- \(Y = \beta_0 + \beta_1X + \beta_2X^2 + \beta_3\sqrt{X} + \epsilon\)
- A nonlinear relationship between \(X\) and \(Y\) can be modeled using a linear regression.
-
Nonlinear Regression: \(Y\) is NOT linear in unknown parameters.
- \(Y = \frac{\beta_0}{1 + e ^{-\beta_1X}} + \epsilon\)
- \(Y = \beta_0e ^{-\beta_1X}\cdot\epsilon\)
👉 Some nonlinear models can be transformed to an equivalent linear model.
Which nonlinear model above can be transformed into a linear model?
Linear vs. Nonlinear Models